Thermistors and RTDs are devices used to measure temperature in modern Heating, Ventilating, Air Conditioning and Refrigeration (HVAC/R) systems. The electrical resistance of both devices is determined by their temperature. Measuring each device’s resistance allows one to determine the ambient temperature of either sensor. There are trade offs with each device, let’s see what they are.
What is an RTD, how is it defined and what is its ideal accuracy?
It has been known for several hundred years that metals increase in resistance with an increase in temperature. Resistance Temperature Detectors (RTD) are metal-based temperature sensors that exploit this resistance change. RTDs can be made from many different metals (see Table 1).
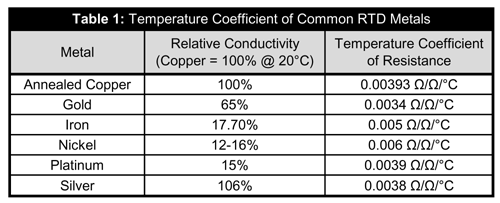
The temperature coefficient of resistance is defined as the resistance of the RTD at 100°C minus the resistance at 0°C divided by 100. The result is then divided by the resistance at 0°C. The temperature coefficient of resistance is the average resistance change from 0°C to 100C°, the actual change for each and every degree from 0°C to 100°C is very close but not identical to it.
Copper has the most linear change in resistance for a given temperature change. Copper’s low resistance makes it difficult to measure small changes in temperature. Nickel has a large change in resistance with a temperature change. Nickel is not a very stable material; its resistance varies considerably from batch to batch. While nickel is much less expensive than platinum, the added processes needed to stabilize nickel makes nickel sensors more expensive than platinum.
Platinum has become the defacto standard in precision thermometry. It has a reasonably high resistance, has a good temperature coefficient, does not react with most contaminant gasses in air and is extremely stable from batch to batch.
In 1871 Werner von Siemens invented the Platinum Resistance Temperature Detector and presented a three term interpolation formula. Siemens’ RTD rapidly fell out of favor due to the instability of the temperature reading.
Hugh Longbourne Callendar developed the first commercially successful platinum RTD in 1885. Callendar discovered that the insulator Siemens used embrittled the platinum causing internal stresses that produced the temperature instability. Callendar changed the insulator material and annealed the RTD at temperatures above the highest desired measurement temperature.
In 1886 Callendar authored a paper discussing his RTD and presented a third order equation that defined the resistance of the RTD for the temperature range of 0 to 550°C. In 1925 Milton S. Van Dusen, a researcher at the National Bureau of Standards – now NIST, extended the formula to -200°C while researching test methods for refrigeration insulation.
The Callendar-Van Dusen equation has been around for 100 years, even though it is not the best fit for platinum RTD’s. Callendar and Van Dusen performed their work well before the advent of modern digital computers. They could not use much more than a third order equation since they had to solve the equation by hand. They used an equation that was reasonably accurate and could be solved in a human lifetime.
In 1968 the International Electrotechnical Commission recognizing of the short comings of the Callendar-Van Dusen equation defined a 20 term polynomial equation for the resistance versus temperature curve for 100 Ohm platinum RTD’s (For 1,000 Ohm RTD’s just multiply by ten.). In Callendar and Van Dusen’s day a 20 term polynomial would have taken several days to solve per temperature point. The arrival of the digital computer makes solving such an equation trivial.
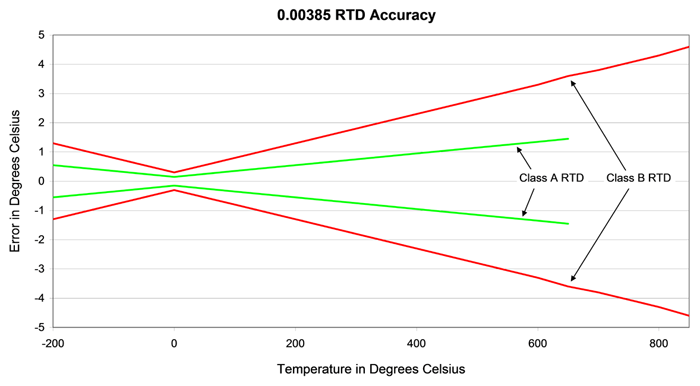
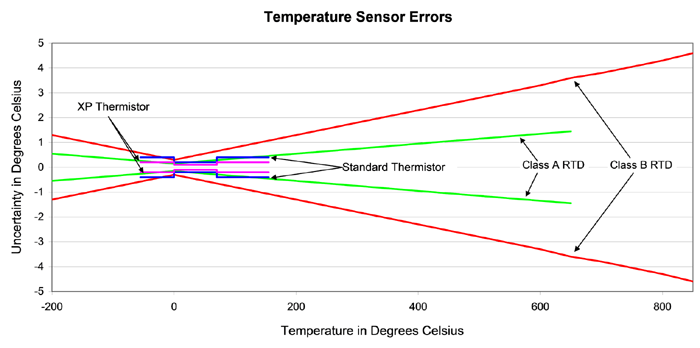
IEC 751 is the International Electrotechnical Commision’s standard that defines the temperature versus resistance for 100 Ω, 0.00385 Ω/Ω/°C platinum RTDs. 1,000 Ω, 0.00385 Ω/Ω/°C platinum RTDs are defined as ten times the IEC 751 specification. IEC 751 defines two classes of RTD; class A and class B. Class A RTDs operate over the temperature range of -200°C to 650°C. Class B RTDs operate over the temperature range of -200°C to 850°C. Class B RTDs have about twice the uncertainty of class A RTDs. See Fig 1.
The uncertainty equations for class A and class B RTDs are;
Permissible uncertainty – Class A °C = ±(0.15 + 0.002T)
Permissible uncertainty – Class B °C = ±(0.3 + 0.005T)
Where T = desired temperature in degrees Celsius.
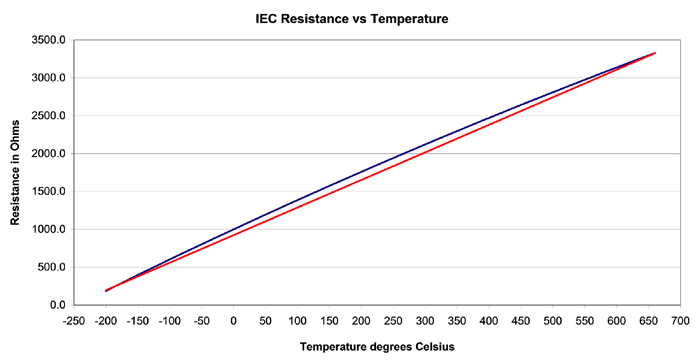
The RTD transfer function can vary anywhere between the limit lines of Fig 1. The transfer function of an RTD is not perfectly linear. Careful examination of the resistance versus temperature table shows a slight “bow” of about 0.45°C for every 100°C. Fig 2 shows the 1KΩ 0.00385 RTD resistance versus temperature curve with the blue line, the red line shows an ideal straight line response.
What is a Thermistor how is it defined and what is its ideal accuracy?
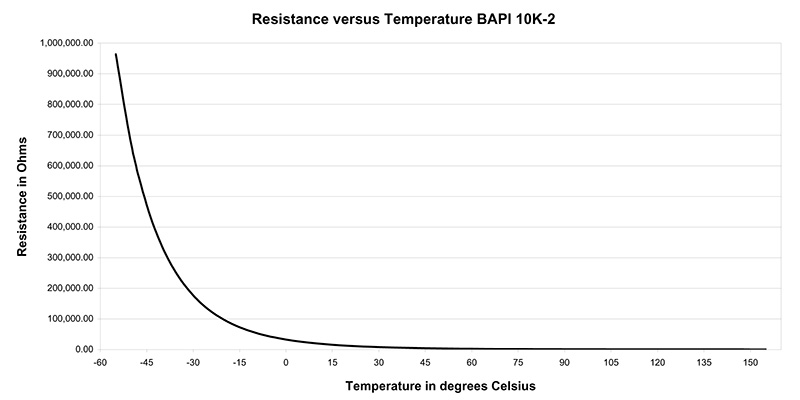
A thermistor is an electrical device that varies its electrical resistance with temperature (Thermistor is short for thermal resistor). The change in resistance with temperature follows the classic logarithmic curve (see Fig 3).
Thermistors are made from mixtures of powdered metal oxides; recipes are closely guarded secrets of the various thermistor manufacturers. The powdered metal oxides are thoroughly mixed and formed into the shape needed for the thermistor’s manufacturing process. The formed metal oxides are heated until the metal oxides melt and turn into a ceramic. Most thermistors are made from thin sheets of ceramic cut into individual sensors. The thermistors are finished by putting leads on them and dipped into epoxy or encapsulated in glass.
Samuel Ruben invented the thermistor in 1930. Mr. Ruben worked for the Vega Manufacturing Corporation. Vega made guitars, banjos and recording machines. Mr. Ruben was working on electronic record stylus pickups when he noticed that the pickup configuration he was working on had a rather large negative temperature coefficient.
Thermistors have come a long way in the past 80 years. According to a researcher at the National Institute of Standards and Technology (NIST), glass encapsulated thermistors are more stable than RTDs. Thermistors, whether glass or epoxy coated can maintain ±0.2°C over large temperature intervals. Extra Precision (XP) thermistors maintain ±0.1°C.
By the 1960s thermistors were main stream sensors. Steinhart and Hart, two researchers at the Woods Hole Oceanographic Institute, published a paper defining a temperature versus resistance formula for thermistors. The Steinhart-Hart equation has become the industry standard equation for thermistors.
The classic Steinhart and Hart equation has the form:
1/T = A0 + A1(lnR) + A3(lnR)3
Where: T = Temperature in Kelvins (Kelvin = Celsius + 273.15)
A0, A1, A3 = Constants derived from thermistor measurements
R = Thermistor’s resistance in Ohms
ln = Natural Log (Log to the Napierian base 2.718281828…)
In practice three thermistor resistance measurements at three defined temperature are made. These temperatures are usually the two endpoints and the center point of the temperature range of interest. The equation hits these three points directly and has a small error over the range. BAPI can provide Steinhart-Hart coefficients for the temperature range of 0°C to 70°C that have uncertainties of 0.01°C or less.
There are no industry or governmental standards for thermistors. There are at least 5 different temperature versus resistance curves for 10K thermistors in the HVAC/R world. All the thermistors have 10,000 Ohms of resistance at 77°F or 25°C, but they vary greatly the further you get away from 77°F. Both BAPI’s 10K-2 and 10K-3 thermistors have 10,000 Ohms of resistance at 77°F. At 32°F (0°C) the 10K-2 thermistor has 32,650 Ohms of resistance and a 10K-3 29,490 Ohms. If a 10K-3 thermistor is substituted for a 10K-2 you could have 6°F of measurement error at 32°F.
Thermistors have a very large resistance change with temperature. Differentiating between one degree and another is relatively easy. This large resistance change limits the temperature range that can be resolved to a fraction of what an RTD can resolve.
How do the accuracies and temperature ranges of RTDs and Thermistors compare?
Thermistors are generally more accurate than Class B RTDs over the thermistors operating temperature range and similar to Class A RTDs.
Are there other application limits for RTDs and Thermistors?
The wiring used to connect the temperature sensor to the measuring device adds resistance and measurement error.
Usually 18 Gauge copper wire is used to connect sensors to their measurement devices. At 20°C (43°F) 18 Gauge wire has a resistance of 6.4 Ohms for every 1000 feet of wire. At 140°F (70°C) 18 Gauge wire has 7.7 Ohms for every 1000 feet of wire. Table 2 shows how much wire may be used if you wish to keep wiring error at ¼ °F or lower.
The wiring errors in Table 2 illustrates why temperature transmitters are used with RTDs. Reasonable wiring lengths are only permissible with transmitters. Transmitters change the RTD resistance into a 4 to 20 mA current signal proportional to the RTDs temperature. A temperature range must be established; a 4 mA output corresponds to the minimum temperature and 20mA corresponds to the maximum temperature. Any intermediate temperature is just a linear proportion from 4 mA to 20mA. Transmitters must be within 10 feet of the RTD’s location. Transmitters may be up to 77,000 feet from the measurement device.

Temperature transmitters can have spans from 16.6°C (30°F) to 555°C (1,000°F) and low, 4mA temperatures, from -150°C (-238°F) to 482°C (900°F). For an extra fee, RTDs and transmitters can be matched to have measurement errors of 0.05°C (0.1°F) across the span.
So what sensor is better, an RTD or a Thermistor?
It depends.
Thermistors cost less than RTDs.
Thermistors measure temperature to the same or better accuracies than RTDs.
Thermistors do not need the extra cost of transmitters.
RTDs have a much larger temperature measurement range than thermistors.
Transmitters add at least $100 to the cost of an RTD.
If you have any questions, please call your BAPI representative.



